Conv. rate with Pluto 🎈

using Plots, LinearAlgebra, PlutoUI

begin
  f(x) = x[1]^2 + γ*x[2]^2
  ∇f(x) = [2*x[1], 2*γ*x[2]]
  opt_step(x, Δ) = - (x[1]*Δ[1] + γ*x[2]*Δ[2])/(Δ[1]^2 + γ*Δ[2]^2)

  function grad_desc(; n_itermax = 40, x0 = [10, 1], ϵ = 1e-1)
    x = zeros(2, n_itermax)
    x[:,1] = x0
    k = 1
    while (norm(∇f(x[:,k])) > ϵ) && (k < n_itermax)
        Δ = - ∇f(x[:,k])
        x[:, k+1] = x[:, k] + opt_step(x[:,k], Δ)*Δ
        k += 1
    end
    x, k
  end
end

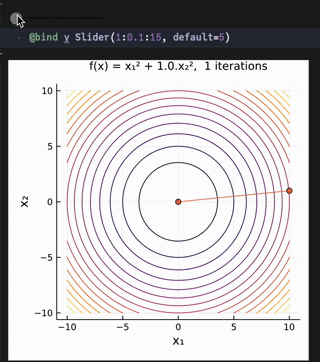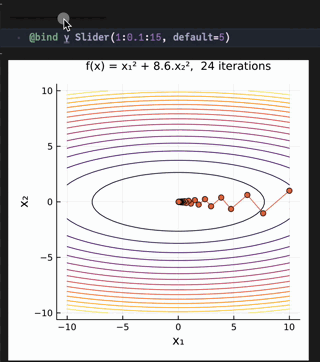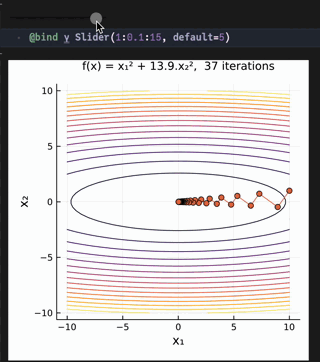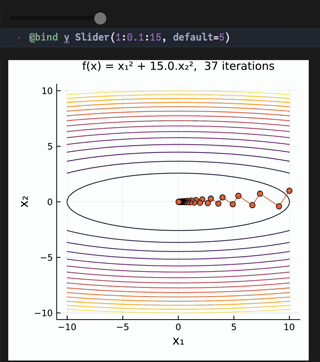
@bind γ Slider(1:0.1:15, default=5)

begin	
x, k_max = grad_desc()
x1_, x2_ = LinRange(-10, 10, 64), LinRange(-10, 10, 64)
contour(x1_, x2_, (x,y)->f([x, y]), xl="x₁", yl= "x₂", rat=:equal, cb=false);
plot!(x[1, 1:k_max], x[2,1:k_max], m=:circle, label="", aspect_ratio=:equal, size=(400,400))
title!("f(x) = x₁² + $γ.x₂²,  $(k_max-1) iterations", titlefontsize=10)
end